When I first started writing embedded software, nearly every project started the same. For the first 3 – 6 months, every single day was spent pouring through microcontroller datasheets and writing a driver for each peripheral that was going to be used on a project. It was a lot of fun. Every microcontroller worked slightly differently than every other and a lot could be learned by observing the differences between how one company implemented a USART versus how another one did. While these activities were eye-opening for a young engineer, by the time a developer has written their third or fourth USART driver, the activity starts to become not only less interesting but a hinderance to getting started on the application code. This is where modern day microcontroller configurators have really started to shine.
A microcontroller configurator is a toolchain component that allows a developer to setup microcontroller peripherals through a nice graphical user interface which in turn generates all the peripheral control code that would have otherwise been written by hand. A microcontroller configurator can dramatically reduce that 3 – 6 months driver development schedule down to a few weeks or less without the need to dig through a thousand pages of technical reference manuals to understand every register bit. Modern configurators don’t just set register values but also provide driver hooks that completely abstract out the low-level hardware.
Microcontroller configurators are by no means a new invention. They’ve been around for at least a decade or more. I recall working with early versions of Freescale Processor Expert on S12X microcontrollers. Back then, configurators were great for understanding the microcontroller and how its peripherals worked. The code they generated though was difficult to read and maintain which was why we would use it for rapid prototyping and then leverage it to hand write our drivers.
Today’s configuration tools though have become quite sophisticated and, in many instances, will meet coding standards such as MISRA-C. In fact, some configurators generate code that reaches quality levels beyond what I see developers hand coding. In any event, there is a trend in the microcontroller space to minimize the developers need to understand the low-level hardware and instead, help them to get up and running with their application code sooner rather than later. This makes a lot of sense given that many modern microcontrollers have grown to levels of sophistication that could require upwards of a year to understand and write code for. Why would a company want to support all that effort, especially if they can get quality code generated from a configuration tool?
There are quite a few configurator tools out there but so far, the ones I’ve encountered have all been produced by the microcontroller manufacturer. For example, Microchip has the Microchip Harmony Configurator, ST Microelectronics has STM32CubeMx and so on and so forth. These tools usually integrate into the manufacturers IDE in some way in order to provide developers with a seamless experience switching between writing their application code and configuring their microcontrollers peripherals and driver interfaces. Every tool looks a little bit different, but since I’ve recently been playing with Microchips Harmony Configurator (MHC), I’ll use it as an example.
A big advantage to these configurator tools is their ability to provide a visual mechanism for configuring the microcontroller. For example, the view below demonstrates how the MHC provides a visual project graph. Developers can easily see which components they have included in their project in addition to connecting dependencies between modules. The image below shows how FreeRTOS is connected to the Harmony Core Service, which connects to a Time service that is generated by a timer.
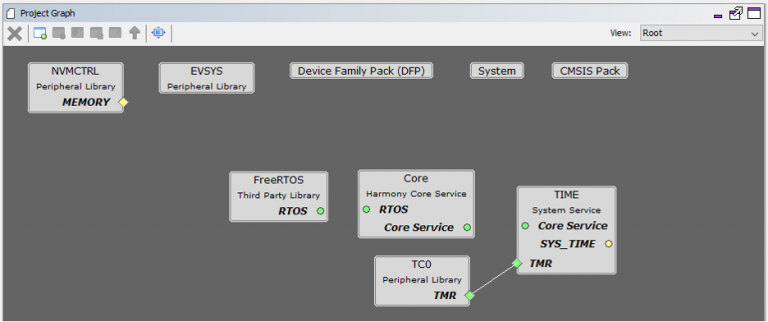
Each of these components in turn can then be selected and configured using a simple check box or dropdown system. For example, the configuration menu for FreeRTOS can be seen in the image below:
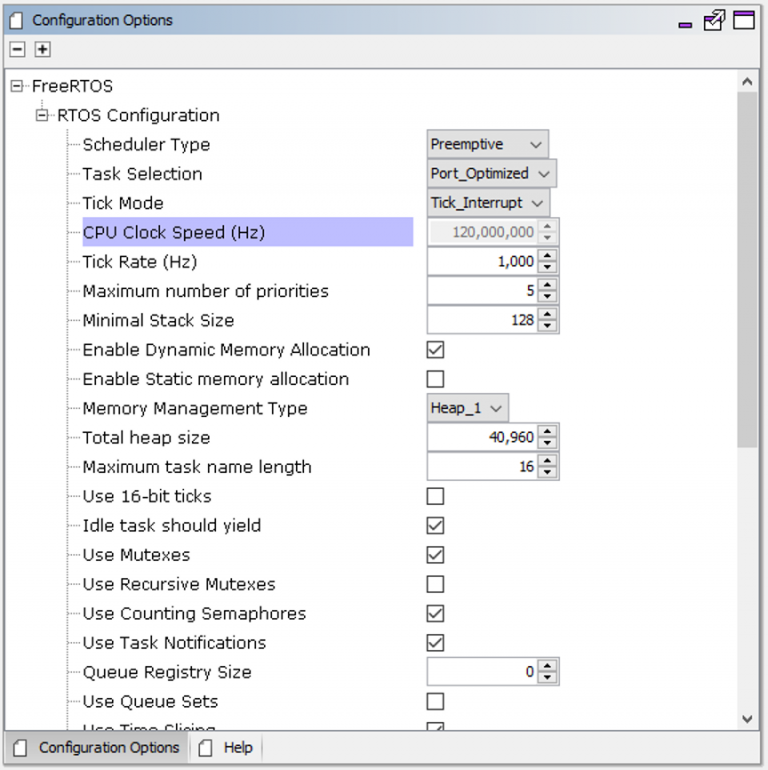
This interface is far easier to use and configure than having to go into a header file and bounce back and forth between the documentation to figure out which definitions need to be added in order to get the feature set that is desired. Once the settings are configured, the code is generated by simply clicking a “generate code” button which generates the code into the project’s directory.
Leveraging a microcontroller configurator can dramatically accelerate software development by decreasing the time spent on setting up drivers and configuring the microcontroller. Developers do need to spend some time getting over the learning curve for the toolchain though. I’ve found that a lot of these tools can be learned within a few days once the proper resources are found. The learning curve usually starts steep, but once the core concept is learned, there is an aha moment that dramatically increases the configuration speed. While each tool is different, they are all designed to help developers get started on their application code sooner rather than later.





